HAMILTONIAN CYCLE
It is a cycle in a graph where every vertex is used once and only once.

Here 123451 is a cycle in which every vertex is used once and only once.so this graph is a Hamiltonian graph.
HAMILTONIAN PATH
It is a path in a graph where vertex is used once and only once

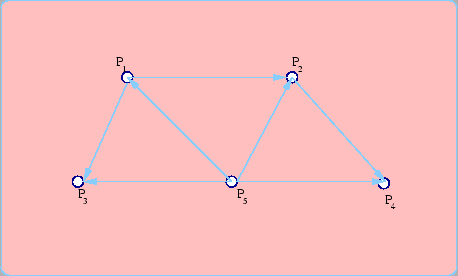
Here 1425631 is a Hamiltonian path.
Theorems associated with Hamiltonian cycle
A graph which is not connected is called a disconnected graph.

Subgraph of a graph
A subgraph of a graph is a graph with either less number of vertices or edges than that of the given graph.
A spanning sub graph of a graph is a sub graph which retains all the vertices of the original graphs.
Component
Given any graph G,a component of G,say G1 is a maximal connected sub graph of G.(ie.G1 should not be a proper sub graph of another connected sub graph of G. If G itself is connected then it has only one component. ie .G itself.
It is a cycle in a graph where every vertex is used once and only once.
Here 123451 is a cycle in which every vertex is used once and only once.so this graph is a Hamiltonian graph.
HAMILTONIAN PATH
It is a path in a graph where vertex is used once and only once
Here 1425631 is a Hamiltonian path.
Theorems associated with Hamiltonian cycle
- Ove's Theorem
- Dirac's Theorem
Connected graphs
A network is said to be connected if between every pair of vertices there exists atleast one path.
A graph which is not connected is called a disconnected graph.
Subgraph of a graph
A subgraph of a graph is a graph with either less number of vertices or edges than that of the given graph.
A spanning sub graph of a graph is a sub graph which retains all the vertices of the original graphs.
Component
Given any graph G,a component of G,say G1 is a maximal connected sub graph of G.(ie.G1 should not be a proper sub graph of another connected sub graph of G. If G itself is connected then it has only one component. ie .G itself.
No comments:
Post a Comment